懒人问大模型要自动化解几何题给出逐步思路的方案

虽然已经很老了，但对中学级别的平面几何定理的证明仍然怀有敬畏之心。自动化的方法，大语言模型AlphaGeometry成果，似乎超越了“数学机械化”的思路了。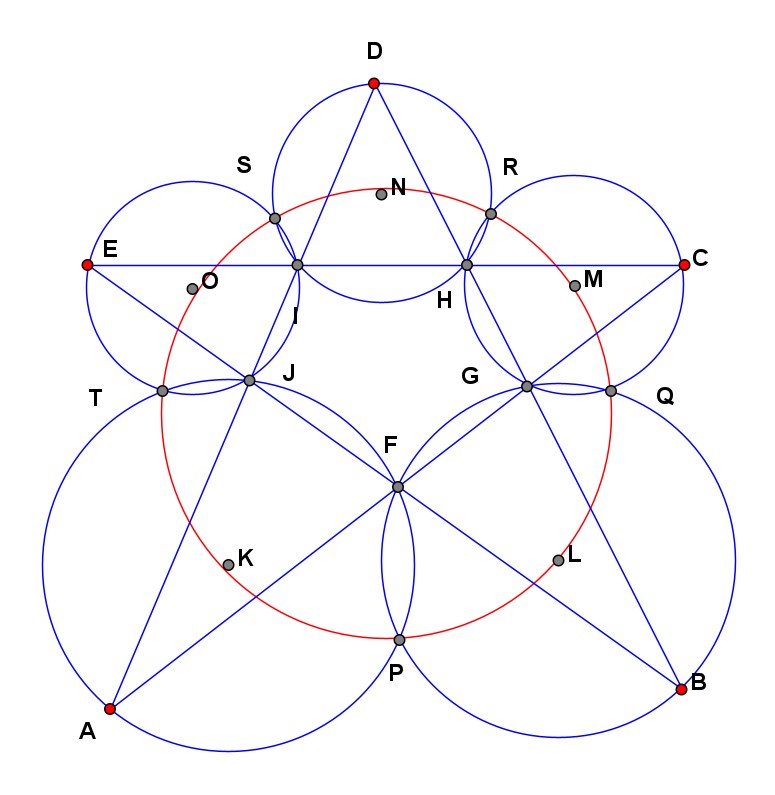

五圆问题（输出结果/已解决/5circles-ddar-ok.log）：

A、B、C、D、E 构成五边形的五个顶点。F、G、H、I、J 为其对角线的交点。五个三角形 AJF、BFG 等的外接圆，除交点 F、G、H、I、J 外，还相交于五个点 P、Q、R、S、T。需要证明 P、Q、R、S、T 五点共圆。

手动求解五圆问题

结果表明，此问题无需引入辅助点即可通过 DD+AR 方法求解，单 CPU 耗时 6 分钟。由于图中涉及众多点且难以直观展现全部几何关系，这对人工证明颇具挑战。该案例充分展示了 DD+AR 几何引擎的强大求解能力。

The 5-Circles Problem (outputs/solved/5circles-ddar-ok.log):

A, B, C, D, E are vertices of a pentagon. F, G, H, I, J are
intersections of their diagonals. 5 circumcircles of triangles AJF,
BFG etc. intersect at 5 points P, Q, R, S, T, in addition to F, G, H,
I, J. Prove that P, Q, R, S, T are concyclic.

5circles-manual

It turns out no auxiliary point is needed for this problem, it can be
solved by DD+AR, taking 6 minutes with 1 CPU in use. This problem is
not easy for humans given there are many points on the diagram and
it’s not easy to see all the relationships between them. This shows
the power of the DD+AR engine.

以下是其中一个答案：

AG4Masses 项目使用指南：让 AlphaGeometry 在普通电脑上运行

AG4Masses 是 Google DeepMind 开源的 AlphaGeometry 项目的一个优化分支，目标是将性能提升约100倍，使普通用户也能在日常硬件上解决IMO级别的几何问题。

为什么需要 AG4Masses？

原始 AlphaGeometry 系统需要强大的计算资源：

• 4个GPU V100
• 最多250个CPU
• 仍然需要1.5小时解决IMO问题

AG4Masses 优化后可在普通家用硬件运行：

• 4-8个逻辑CPU
• 16-32GB内存
• 无需高端GPU
• 一天内解决IMO级别问题

系统要求

• 操作系统：Linux（推荐 Ubuntu 22.04 或 Mint 21.3）
• Python版本：3.10（对其他版本兼容性较差）
• 必要包：

  sudo apt update
  sudo apt install python3-virtualenv python3-tk
  

安装与配置

1. 目录结构设置

建议将文件分三个目录存放：

# 输出文件目录
TESTDIR=$HOME/ag4mtest
# AG4Masses源代码目录
AG4MDIR=$HOME/ag4masses
# 外部库目录（包括模型权重）
AGLIB=$HOME/aglib

2. 获取源代码

cd $HOME
git clone https://github.com/tpgh24/ag4masses.git
mkdir $AGLIB
cd $AGLIB
git clone https://github.com/google-research/meliad
mkdir $AGLIB/ag_ckpt_vocab

3. 下载模型文件

从 https://bit.ly/alphageometry 下载以下文件到 $AGLIB/ag_ckpt_vocab：

• checkpoint_10999999
• geometry.757.model
• geometry.757.vocab

4. 创建虚拟环境

virtualenv -p python3 $HOME/pyve
. $HOME/pyve/bin/activate
cd $AG4MDIR/alphageometry
pip install --require-hashes --no-deps -r requirements.txt

5. 验证安装

cd $TESTDIR
$AG4MDIR/utils/run_tests.sh

除最后一个测试外，其他测试都应该通过。

运行 AG4Masses

1. 配置运行参数

编辑 $AG4MDIR/utils/run.sh 文件，设置关键参数：

# 文件路径配置
TESTDIR=$HOME/ag4mtest
AG4MDIR=$HOME/ag4masses
AGLIB=$HOME/aglib

# 问题选择
PROB_FILE=$AG4MDIR/data/ag4m_problems.txt  # 问题文件
PROB="napoleon"  # 具体问题名称

# 模型选择
MODEL="alphageometry"  # 或 "ddar"（只用符号引擎）

# 性能参数（根据你的硬件调整）
BATCH_SIZE=8    # 每次LM查询的输出数量
BEAM_SIZE=32    # 广度优先搜索队列大小
DEPTH=8         # 搜索深度（要添加的辅助点数量）
NWORKERS=1      # 并行工作进程数

2. 启动求解

cd $TESTDIR
$AG4MDIR/utils/run.sh

结果将输出到：

• 标准输出：终端和 $TESTDIR/ag.err
• 问题解决方案：$TESTDIR/ag.out（如果成功解决）

问题格式说明

AG4Masses 使用特定语法定义几何问题：

问题名称
前提条件 ? 结论

示例：垂心问题

orthocenter
a b c = triangle; h = on_tline b a c, on_tline c a b ? perp a h b c

语法要点：

• 前提条件：使用分号分隔多个点的构造
• 动作：定义在 alphageometry/defs.txt 中，如 on_tline（在垂直线上）
• 结论：支持多种几何关系：
  • coll a b c：三点共线
  • cong a b c d：线段ab与cd等长
  • perp a b c d：线段ab与cd垂直
  • para a b c d：线段ab与cd平行
  • cyclic a b c d：四点共圆
  • eqangle a b c d p q r s：角度相等

重要提示：语法对空格敏感，特别是在行尾。问题格式错误通常会导致程序冻结。

内置问题集

AG4Masses 提供多个问题集：

1. data/ag4m_problems.txt：经典几何问题

   • 五圆问题
   • 拿破仑问题
   • 蝴蝶问题
   • 塞瓦定理

2. alphageometry/examples.txt：基础测试示例

3. alphageometry/imo_ag_30.txt：30个IMO几何问题

4. alphageometry/jgex_ag_231.txt：231个来自Java-Geometry-Expert的问题

实用工具

项目提供几个有用的脚本：

• utils/checkprog.sh：监控运行进度
• utils/mklog.py：处理日志文件，生成更清晰的版本
• utils/run.sh：主运行脚本，已配置好环境变量

2025年1月新增功能

• Kaggle Notebook：可在Kaggle上运行，利用其免费资源：

  • 2个Nvidia T4 GPU
  • 4个虚拟CPU
  • 29GB内存
  • 每小时可处理约200个图形

• 多CPU支持：在对称多处理器机器上使用多个CPU提高速度

• 增强的鲁棒性：处理了许多会导致AlphaGeometry中止的错误情况

典型用例

拿破仑问题：对于任意三角形ABC，构造三个等边三角形，证明它们的中心构成等边三角形。

• 简单版本：无需辅助点，DD+AR引擎6分钟内解决
• 挑战版本：需要辅助点，AG4Masses在尝试约360个图形后找到解决方案

蝴蝶问题：在一个圆中，M是弦PQ的中点，AB和CD是通过M的两条弦。AD和BC分别与PQ相交于X和Y。证明M是XY的中点。

AG4Masses已在普通家用硬件上成功解决此问题。

---

通过AG4Masses，你可以在普通电脑上体验这个曾需要超级计算资源的先进几何定理证明系统。项目仍在积极开发中，欢迎贡献代码或加入讨论！

下面我来一步步介绍如何使用这个项目：AG4Masses（即 tpgh24/ag4masses —— “Making AlphaGeometry accessible to the Masses”）来运行 AlphaGeometry。如果你熟悉 Python／Linux 环境的话，会比较顺利。以下是整理好的流程 + 注意事项，适合有技术背景的来理解使用。

---

1. 项目简介

这个项目是 Google DeepMind 开源的 AlphaGeometry 的一个“可普及”版本。原版 AlphaGeometry 需要极强硬件（论文中提到：4 GPU V100 + 250 CPU 才能在约 1.5 小时内解决 IMO 水平几何题）(GitHub)。
而 AG4Masses 的目的是在较为常见的硬件（例如 4-8 逻辑 CPU + 16-32 GB RAM，无高端 GPU）上提升其能力约百倍，使其能处理大部分平面几何题目。(GitHub)

---

2. 环境要求与准备

根据 README 的说明，以下是建议的系统／软件环境。(GitHub)

• Linux 系统（作者在 Ubuntu 22.04 或 Mint 21.3 上测试通过）(GitHub)
• Python 3.10（作者提到在 Python 3.11 上依赖可能出问题）(GitHub)
• 虚拟环境（virtualenv）建议使用，便于隔离依赖。
• 安装一些系统包，比如 python3-virtualenv、python3-tk 等。(GitHub)
• 下载项目本体 + 其依赖的语言模型权重文件。

---

3. 下载与安装步骤

在你的 Linux 环境中，你可以按如下步骤操作：

1. 选择一个工作目录，比如 ~/ag4mtest 或 ~/ag4masses。

2. 克隆 AG4Masses 仓库：

   cd ~
   git clone https://github.com/tpgh24/ag4masses.git
   

   (GitHub)

3. 创建一个用于放置外部库／模型的目录，例如 ~/aglib：

   mkdir ~/aglib
   cd ~/aglib
   git clone https://github.com/google-research/meliad
   

   (GitHub)

4. 在 ~/aglib/ag_ckpt_vocab 下面下载模型权重／词汇表文件（Google Drive 提供）包括 checkpoint_10999999, geometry.757.model, geometry.757.vocab。(GitHub)

5. 创建 Python 虚拟环境并激活：

   virtualenv -p python3 ~/pyve
   source ~/pyve/bin/activate
   

   然后进入 ag4masses/alphageometry 目录，安装 Python 依赖：

   pip install --require-hashes --no-deps -r requirements.txt
   

   （注意标记 --no-deps，作者指出如果不加可能安装失败）(GitHub)

---

4. 配置 & 运行测试

• 编辑 utils/run_test.sh，将其中设置的 TESTDIR, AG4MDIR, AGLIB 环境变量改为你自己的路径。(GitHub)

• 在测试目录 TESTDIR 下运行：

  cd $TESTDIR
  $AG4MDIR/utils/run_tests.sh
  

  这会运行内部测试，检查安装是否正确。(GitHub)

• 如果测试基本通过（除了某个数值稳定性较弱的测试）就可以继续下一步。

---

5. 运行实际几何题目

• 编辑 utils/run.sh，同样设定好 TESTDIR, AG4MDIR, AGLIB。(GitHub)

• 在 run.sh 中还需要设定你要运行的题目文件：将环境变量 PROB_FILE 和 PROB 指向你选的题目集合文件，比如：

  • data/ag4m_problems.txt：AG4Masses 自己提供的额外题集。(GitHub)
  • alphageometry/examples.txt：AlphaGeometry 原始提供的示例。(GitHub)

• 设置模型类型：环境变量 MODEL 可取值：

  • ddar：仅使用 DD+AR 引擎（无自动加辅助点）
  • alphageometry：使用含语言模型辅助加辅助点的模式（AG4Masses 模式）(GitHub)

• 可配置参数包括（在 run.sh 中注释有说明）：

  BATCH_SIZE  # 每次 LM 查询输出数量  
  BEAM_SIZE   # BFS 队列大小  
  DEPTH       # 搜索深度（即辅助点最大数）  
  NWORKERS    # 并行 worker 数量  
  

  作者建议：例如 128 GB 机器 + 16 逻辑 CPU 时，使用 NWORKERS=8, BATCH_SIZE=24。但也提醒：较大 BATCH_SIZE、NWORKERS 可能导致内存溢出。(GitHub)

• 例如你可能运行命令（在 run.sh 中）类似：

  MODEL=alphageometry
  BATCH_SIZE=8
  BEAM_SIZE=32
  DEPTH=8
  NWORKERS=1
  # 然后执行脚本
  ./utils/run.sh
  

  输出会写入标准输出、stderr 和日志文件（比如 ag.err, ag.out）(GitHub)

---

6. 问题定义语言（Problem Definition Language）

由于你有数学背景，这部分你会觉得像 DSL（领域专用语言）定义。README 中有详细说明：(GitHub)

• 每个几何题录入两行：第一行是问题名字，第二行是构造／结论语句。

• 在第二行中，前半部分是“前提”（premises），定义点、直线、圆、辅助点构造；后半部分（用 ? 分隔）是“结论”（conclusion）。(GitHub)

• 前提中多个构造子句用 ; 分隔。构造子句像： a b c = triangle 或 h = on_tline b a c, on_tline c a b。(GitHub)

• “Action” 例如： on_tline, intersection_ll 等，定义在 defs.txt 中。(GitHub)

• 结论可用的类型包括（但不限于）：

  • coll a b c ：a, b, c 三点共线
  • cong a b c e ：线段 ab 与 cd 长度相等
  • cyclic a b c d ：四点共圆
  • eqangle … ：两个角相等（带方向）
  • para a b c d ：线段 ab 与 cd 平行
  • perp a b c d ：线段 ab 与 cd 垂直 (GitHub)

• 注意事项：角带方向（sign）必须小心。(GitHub)

• 如果你只是想先验证语法／生成图示，可将结论改为比较“简单无意义”的形式（比如 cong a b a b），如果能成功则说明语法没问题。(GitHub)

---

7. 与你相关的注意事项 + 推荐技巧

考虑到你过去的经验，这里是几何 AI 项目，可能是额外兴趣。以下是一些建议：

• 你可以先在虚拟机或 WSL (如果你在 Windows 上) 上部署一个 Ubuntu 安装环境，安装 Python 3.10。
• 推荐先用简单几何题目做实验，熟悉 DSL 语法以及脚本运行流程，然后再尝试复杂题目。
• 留意：辅助点（auxiliary points）搜索可能非常耗时，尤其题目复杂时。AG4Masses 提到了一个题目尝试了约 7500-9500 种图形仍未解决。(GitHub)
• 如果你对 Mathematica 感兴趣，也可以考虑将该工具生成的几何构造图和 AlphaGeometry 的输出结果做比对，可能有助于理解其构造策略。
• 如果你运行过程中结果失败或运行时间特别长，建议先降低 DEPTH 值、降低 BATCH_SIZE、或切换为 MODEL=ddar（即只用 DD+AR 引擎）来验证是否为语法或环境问题。
• 记录好日志文件（如 outputs/solved, outputs/unsolved）以及辅助点搜索记录，AG4Masses 项目也鼓励用户反馈和参与。(GitHub)

---

如果你愿意，我可以帮你 生成一个具体的运行示例脚本（包括环境变量、shell 脚本、问题定义文件示例）和 一个几何题目的完整流程（从 DSL 编码到运行结果分析），你看要不要？